
[ C.S 지식 정리 : 자료 구조 ] 자료구조와 알고리즘,
'시간 복잡도' 에 대한 이해 (Big-O 표기법)
∇ 자료 구조 : 시간복잡도에 대한 기초 지식 정리
목 차
1. Data(자료)란?
2. 자료구조(Data Sctructure)란?
3. 추상 자료형 ( Abstract Data Type )
4. 알고리즘 ( Algorithm )
5. 시간 복잡도 & 공간 복잡도
6. 시간 복잡도 함수
7. Big-O표기법 ( Big-O Notation )
8. Big-O 표기법 특징
9. Big-O 표기법의 수학적 정의
10. Big-O 표기법의 종류 및 비교.
11. Big-Ω & Big-θ 표기법
12. Big-0 표기법 사용
13. 최선, 평균 ,최악의 경우
1. Data ( 자료 ) 란?
facts and statistics collected together for reference or analysis
※ 참고 또는 분석을 위해 수집된 사실과 통계 !
즉, "데이터"는 현실 세계로부터 수집되는 사실(fact)이나 값(value)
또는 이들의 집합이자 가공되지 전의 상태를 의미합니다.
= > 특정 목적을 위해서 데이터를 가공하고 해석한 후의 상태를 "정보(Information)" 이라고 합니다.
2. 자료구조( Data Structure ) 란?
※ 자료구조란, " 데이터를 표현하거나 저장하는 방법 " 입니다.
@ 효과적으로 설계된 자료구조는 프로그램의 실행시간을 단축시키고 메모리 용량을 최소한으로 사용하여
연산 속도를 높여줍니다.
@ 프로그램 설계 시 가장 우선적으로 어떠한 종류의 자료구조를 선택해야 할지를 고려해야 합니다.
@ 연산 방법과 코드의 목적 등에 따라서 다양한 자료구조가 있으며, 일반적으로 아래 표와 같이 분류합니다.
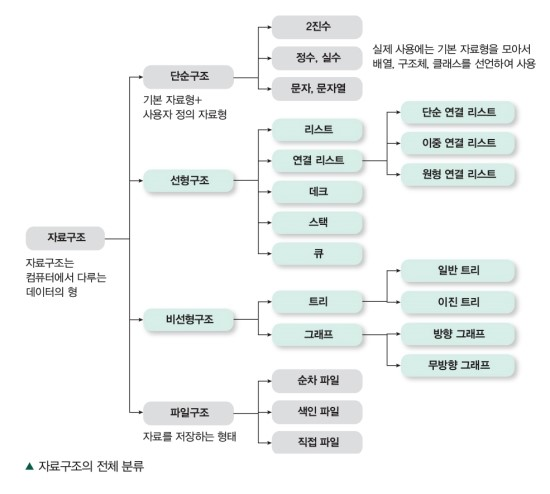
☆ 단순 구조는 프로그래밍에서 사용되는 기본적인 자료형을 의미합니다.
☆ 선형 구조의 자료구조는 데이터 간의 관계가 1:1 로 형성되어서, 선형적으로 나열되는 구조를 가집니다.
☆ 비선형 구조는 데이터 간의 관계가 1:n 또는 n:m으로 형되는 자료 구조입니다.
3. 추상 자료형 ( Abstract Data Type )
※ 자료형이란, 데이터와 연산의 집합을 의미합니다.
흔히 사용하는 자료형인 ' int ' 의 경우 , 4byte로 표현 가능한 정수 범위를 데이터로 가지며,
산술 연산자 [ + , - , *, / , % ] 로 연산이 가능합니다.
§ " 추상 자료형 " 은 데이터 타입과 그 데이터와 관계된 연산들을 '수학'적으로 정의한 것 입니다.
- > ' 기능의 구현은 정의하지 않고 ' , 데이터의 형태와 그 데이터의 연산만 추상적으로 정의를 한 상태 !
- > "2"에서 정의한 "자료구조"는 추상 자료형이 정의한 연산들을, 구현한 구현체.
☆ "객체지향 프로그래밍 ( OOP ) 에서의 '클래스(Class)' 개념과 유사.
4. 알고리즘 ( Algorithm )
- 자료구조가 데이터를 표현하거나 저장하는 방법이라면,
알고리즘은 이렇게 저장시킨 데이터를 활용하여 문제를 해결하기 위한 절차나 방법을 의미합니다.
☆ 좋은 알고리즘을 만들기 위해서 만족시켜야 할 "5가지 조건" 이 있습니다.
- 입력 : 0 개 이상의 입력이 존재하여야 합니다.
- 출력 : 1 개 이상의 출력이 존재하여야 합니다.
- 명확성: 1 개 이상의 출력이 존재하여야 합니다.
- 유한성: 한정된 횟수의 단계 후에는 반드시 종료되어야 합니다.
- 유효성: 각 명령어들은 실행 가능한 연산이어야 합니다.
☆ 알고리즘을 표현하는 4가지 방법.
- 자연어
: 인간이 이해하기 가장 쉬운 말로 설명되어 있는 형태이며, 단어들을 정확하게 정의해주지 않으면 의미 전달이 모호해질 수 있습니다.
- Flowchart(순서도)
: 직관적이며 이해하기 쉽지만, 복잡한 알고리즘의 경우에는 작성이 복잡해집니다.
- Pseudo-code(의사코드)
: 프로그래밍 코드를 흉내내어서 보다 간단하게 표현할 수 있는 코드이며,
알고리즘의 핵심 내용에만 집중할 수 있습니다.
- Computer Language(프로그래밍 언어)
: 우리가 사용하는 코딩 언어들입니다. 표현하고자 하는 대로 가장 정확하게 알고리즘을 기술할 수 있지만,
많은 코드로 인해 알고리즘의 해심 내용의 이해를 방해할 수 있습니다.
5. 시간 복잡도 & 공간 복잡도
□ 효율적인 알고리즘을 만들기 위해서는, 알고리즘의 성능을 분석하고 평가할 수 있어야 합니다.
□ 컴퓨터상에서는 시간과 메모리 두 자원이 알고리즘의 효율성을 측정하는 척도가 됩니다.
□ 알고리즘의 수행 시간을 분석한 결과 = "시간 복잡도 ( time complecity ) "
- > 알고리즘이 시작되어서 완료되는 데까지 걸리는 시간을 의미합니다.
( 실제론, 각 컴퓨팅 하드웨어의 성능 혹은 언어 성능에 따라 속도가 달라지기 때문에 고려 X)
== > 그러므로, 알고리즘에서 "시간 복잡도 " = " 실행 명령어의 실행 횟수 "
□ 메모리 사용량을 분석한 결과 = " 공간 복잡도 ( spcae complectiy ) "
== > 알고리즘에서의 공간 복잡도 = " 메모리 사용량 "
6. 시간 복잡도 함수.
○ 알고리즘 수행에 필요한 전체 연산 수를 계산하면, 실행 시간을 구할 수 있으며
이를 함수로 나타낼 수 있습니다.
ex) (주석은 실행 빈도 수 )
void f(int n){
int cnt = 0; // 1
int sum = 0; // 1
for(int i=0; i<n; i++){
cnt++; // n
sum += i; // n
}
}위 알고리즘의 시간 복잡도 함수는 f(n)=2n+2 입니다.
- n은 입력 개수를 뜻하며, n과 시간은 정비례 관계입니다 ( n이 증가하면, 그에 비례하여 시간도 증가 )
7. Big-O 표기법 ( Big -O Notation )
☆ 알고리즘의 시간복잡도와 공간복잡도를 표현하는 대표적인 방법에는, " Big-O 표기법 " 이 있습니다.
- Big-O 표기법은 알고리즘 실행에 있어서 " 최악의 경우"을 상정해서 나타냅니다.
= > 시간 또는 공간에 있어서 '상한성'을 두는 것.
8. Big-O 표기법 특징
ex ) 이라는 시간 복잡도 함수가 있다고 가정해보자.
입력값 n이 증가할수록, 차수가 가장 큰 항이 결과값에 가장 큰 영향을 미치며, 다른 항들은 상대적으로 무시됩니다.
Big-O 표기법에서는 " 영향력이 없는 항과 상수 계수를 제거하고
실질적으로 가장 영향력이 큰 항(최고차항)으로만 시간 복잡도를 표현합니다.
◇ 원 함수를 단순화시켜서, 최고차항의 차수만을 고려하는 표기법을 '점근식 표기법(asymptotic notation)이라고 함
9. Big-O 표기법의 수학적 정의
두 개의 함수 과 이 주어졌을 때, 모든 에 대하여 을 만족하는
2개의 상수 와 가 존재하면 이다.
f(n)은 알고리즘의 시간복잡도를 의미하며 g(n)은 가장 영향력 있는 항을 뜻합니다.
예를 들어보자.
- f(n)=2n+1 이면 O(n)이다. (g(n) = n)
왜냐하면 n₀=2, c=3일 때, n≥2에 대하여 2n + 1 ≤ 3·n을 만족하기 때문입니다. - f(n)=3n²+100 이면 O(n²)이다. (g(n) = n²)
왜냐하면 n₀=100, c=5일 때, n≥100에 대하여 3n² + 100 ≤ 5·n²을 만족하기 때문입니다.
이걸 그래프로 표현해보면,

위에서 언급했듯이 은 알고리즘의 시간복잡도를 보여주는 그래프이며 최악의 경우를 나타냅니다.
위 그래프에서 입력값 이 를 넘어갈 때부터 알고리즘 은 절대로 상한선 을 넘을 수 없음을 알 수 있습니다.
따라서 Big-O 표기법으로 알고리즘의 시간복잡도를 간단하게 표현할 수 있는 것입니다.
10. Big-O 표기법의 종류 및 비교


n 값이 작을 때는 알고리즘 간의 차이가 미미하지만, n값이 무한대로 커질수록 알고리즘 수행 시간은 급격히 차이납니다.
☆ 각 자료구조 연산 별 시간복잡도

11. Big-Ω & Big-θ 표기법
Big-O(Big-Omicron)는 시간 또는 공간의 상한을 나타냅니다.
Big-Ω(Big-Omega)는 반대로 하한을 나타냅니다.
Big-θ(Big-Theta)는 O와 Ω를 동시에 만족하는 경우를 의미 합니다.
즉, 어떤 알고리즘이 O(n)과 Ω(n)을 모두 만족해야만 θ(n)을 만족하는 것 입니다.
12. Big-O 표기법 사용
- Big-Ω와 Big-θ 표기법이 있지만, 대부분의 경우 알고리즘의 시간복잡도를 표현할 때 Big-O 표기법만 사용합니다.\\
ex ) 배열의 값을 찾는 알고리즘의 경우, 시간복잡도를 O(n) 으로 표현합니다.
그러나 사실 Big-O는 함수의 상한만 표시하면 되므로 O(n²), 심지어 O(n!)로 표현해도 문제는 없다고 합니다.
따라서 실제로는 Big-θ의 개념을 가지는 Big-O를 사용합니다.
즉, 함수의 상한에 존재하는 시간복잡도 중 가장 작은 시간복잡도로 표현하는 것입니다.
13. 최선, 평균, 최악의 경우
- 평균은 계산하기가 까다로우므로 패스
- ex) 배열 내의 어떠한 x값을 찾을 때 첫번째 index부터 순차적으로 찾는 알고리즘.
- > 최선 : 첫번째 index에 x 값이 위치하여 한번에 찾을 수 있을 것.
- > 최악 : 마지막 index에 x값이 위치하여 배열의 크기(n)만큼 전부 찾아야 할 것.
'면접준비[프론트,백,데이터,CS] > CS 정리' 카테고리의 다른 글
| [ C.S 지식 정리 : 자료 구조 ] 자료구조 & 알고리즘의 정의. (1) | 2024.12.13 |
|---|---|
| [ C.S 지식 정리 : 자료 구조 ] 배열(Array) & 연결-리스트(LinkedList) (0) | 2024.11.16 |
| [ C.S 지식 정리 : 자료 구조 ] 알고리즘 공부 하기 전 필요한, 자료구조 기초 지식들. (0) | 2024.11.16 |
| [ C.S 지식 정리 : 디자인 패턴 ] 디자인 패턴 : MVC 패턴이란? (1) | 2024.11.02 |
| [ C.S 지식 : 디자인패턴 ] 디자인 패턴 [ Design Pattern ]이란? (0) | 2024.11.02 |