
[ Data Science ] 데이터 싸이언스 공부_통계학_01 : 평균, 분산, 표준편차 등등.

∇ 기술통계학이란
◇ "통계학"은 크게 두 가지 분야로 구분됩니다.
-> 하나는 " 기술 통계학" 이고, 다른 하나는 "추론 통계학" 입니다.
◎ 기술통계학
:: 기술통계학은 집단(우리가 보유한 통계자료)의 특성을 기술하는 데 목적을 두고 있습니다.
자료의 성질을 기술하는 것이 목적입니다.
- 평균, 분산, 표준편차, 상관계수 등등의
"통계량을 이용해 자료의 분포를 파악" 하고 특성을 기술하는 방법이 있고,
- 도수분포표, 히스토그램, Box-Plot, Steam-and-Lead, 산점도 등
"그림을 이용해 자료의 특성을 요약" 하는 방법이 있습니다.
∇ 기술통계학_주요 통계량 분석 :: 평균, 분산, 표준편차,중위값, 최빈값
1. 평균 [ Mean ] - 산술평균.
:: 데이터의 중심 경향을 나타내는 값으로, 모든 관측값의 합을 데이터의 총 갯수로 나눈 값,

○ 모든 관측치를 더해, 관측치 개수로 나눈 값,
○ 집단의 중심 경향성을 나타냅니다.
○ 기호 μ(뮤)로 표현
ex) {3.0,3.4,3.6,4.1,7.4}

※ 산포도 측정.
2. 분산[ Variance ]
:: 데이터가 평균을 중심으로 얼마나 퍼져 있는가.

○ 데이터가 평균을 중심으로 해서 퍼져있는 정도를 측정.
○ 각 관측치와 평균의 차이(편차)을 제곱해서 계산합니다.
○ 분산이 작을수록 데이터가 평균 주변에 밀집하게 됩니다.
○ 일반화 가능성을 판단하는 중요한 지표.
ex)

3. 표준편차[ Standard Deviation]
○ 분산값의 제곱근입니다.
○ 데이터의 분포가 평균으로부터 얼마나 퍼져있는지를 나타내는 지표입니다.
== 데이터의 변동성을 측정한는데 사용됩니다.
ex)

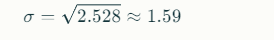
4. 중위값[ Median ]
:: 데이터를 크기순으로 정렬했을 때, 가운데 위치한 값.
- 홀수 개 데이터 : 중앙에 위치한 값
- 짝수 개 데이터 : 중앙 두 값의 평균.
○ 전체 데이터의 정중앙에 위치하는 값.
○ 평균값과 달리 극단값에게 영향을 받지 않습니다.
○ 상위 50% 지점을 나타냅니다.(딱 중앙)
ex) {3.0,3.4,3.6,4.1,7.4}
중앙값 : 3.6
5. 최빈값 [ Mode ]
○ 주어진 데이터 집합에서 가장 자주 나타나는 값.
○ 데이터(자료)의 분포를 파악하는 데 사용.
○ 최빈값은 여러 개의 값에서 동일한 '빈도'로 나타날 때, 여러개가 존재할 수 있으며,
이 경우 다중 최빈값이라고 합니다.
∇ 통계량 해석의 중요성.
○ 단순 평균만으로는 집단의 특성을 완전히 이해할 수 없음.
○ 분산, 중위값 등 다양한 통계량을 종합적으로 분석해야 함.
○ 데이터의 일반화 가능성을 높이기 위해 다각도로 접근.
- 평균은 데이터를 요약하는 대표적인 척도지만 이상치에 민감합니다.
- 중앙값은 이상치에 강건하며 왜곡된 분포에서 유용합니다.
- 최빈값은 범주형 데이터나 특정 값이 자주 반복되는 경우 유용합니다.
- 데이터를 이해할 때는 여러 통계량을 함께 분석하고 시각화를 활용하여 분포를 파악해야 합니다.
@주의사항.
- 이상치(Outliers) 주의
- 데이터의 분포와 특성을 종합적으로 고려,
- 단순 일반화의 위험성을 인식.
,
'Data [ Engineer & Analytics &science ] > Data Science' 카테고리의 다른 글
| [ Data Science ] 데이터 싸이언스 공부_통계학_02 : 변량, 도수, 도수분포표, 상대도수, 히스토그램. (0) | 2025.01.10 |
|---|