
[ Data Science ] 데이터 싸이언스 공부_통계학_02
: 변량, 도수, 도수분포표, 상대도수, 히스토그램.
Ⅰ. 변량 [ Variable ]
- ' 변량 ' 은 연구나 관찰 대상에서 관심을 가지는 속성 또는 특성을 나타냅니다.
- ex) 학생들의 키, 나이, 성적 등은 모두 변량.
-> 이러한 '변량'은 "데이터 분석의 기반"을 형성합니다.
ex) 100명의 학생들의 임의의 점수.

Ⅱ. 도수 [ Frequency ]
※ 도수란,
:: 특정 구간 또는 범주 내에 발생한 관찰값의 수를 의미합니다.
- 도수는 데이터의 분포를 이해하고 시각화하기 위한 핵심 개념입니다.
Ⅲ. 도수 분포표 [ Frequency Distribution Table ]
도수분포표는 변량의 각 값에 대한 도수와 상대도수를 나타내는 표입니다.
-> 데이터의 패턴을 한눈에 파악 가능합니다.

Ⅳ. 상대 도수 [ Relative Frequency ]
상대도수는 특정 도수를 전체 도수로 나눈 비율을 나타냅니다.
-> 데이터의 상대적 분포를 파악하는데 도움이 됩니다.
◇ 상대도수를 사용하는 이유.
1. 비교 용이성
:: 서로 다른 데이터 집단 또는 범주 간에 상대적 크기를 비교할 수 있도록 도와줍니다.
- 도수 분포표의 경우, 도수 자체는 절대적인 수치이지만,
상대도수는 백분율로 표현되어 데이터 집단 간의 상대적 비교를 용이하게 합니다.
2. 데이터 시각화.
:: 상대도수는 그래프나 차트에서 사용하기에 편리합니다.
- 히스토그램, 막대그래프, 원 그래프 등에서
상대도수를 사용하면 각 범주의 상대적 크기를 더 쉽게 비교 가능합니다.
->> 데이터 분포의 모양과 특징을 시각적으로 파악하기 용이해집니다.
3. 정규화
:: 상대도수는 데이터 집합의 크기에 상관없이 상대적 비율을 나타냅니다.
-> 서로 다른 크기의 데이터 집합을 비교하거나, 동일한 데이터 집합의 다른 부분 간의 비교에 유용합니다.
4. 통계 통찰력.
:: 상대도수를 사용하면, 데이터의 특성을 빠르게 이해할 수 있습니다.
-> 특정 범주가 전체 데이터에서 차지하는 상대적 중요성을 파악하고,
이를 통계적 패턴 및 트랜드를 식별하는 데 활용할 수 있습니다.
5. 데이터 분석과 의사결정
:: 상대도수는 데이터 분석 및 의사결정 프로세스에 유용한 정보를 제공합니다.
-> 특정 범주의 상대도수가 높을 때, 해당 범주에 대한 중요성이 강조될 수 있고,
이를 통해 의사결정을 내릴 때 중요한 기준으로 활용됩니다.
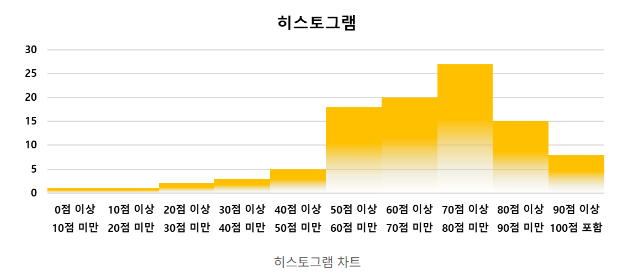
Ⅴ. 히스토그램 [ Histogram ]
※ 히스토그램은 데이터의 도수분포를 시각화한 그래프로,
가로축에는 변량의 범주 또는 구간을,
세로축에는 도수를 표시합니다.
- 히스토그램은 데이터의 분포와 모양을 쉽게 이해할 수 있도록 해줍니다.
'Data [ Engineer & Analytics &science ] > Data Science' 카테고리의 다른 글
| [ Data Science ] 데이터 싸이언스 공부_통계학_01 : 평균, 분산, 표준편차 등등. (0) | 2025.01.08 |
|---|